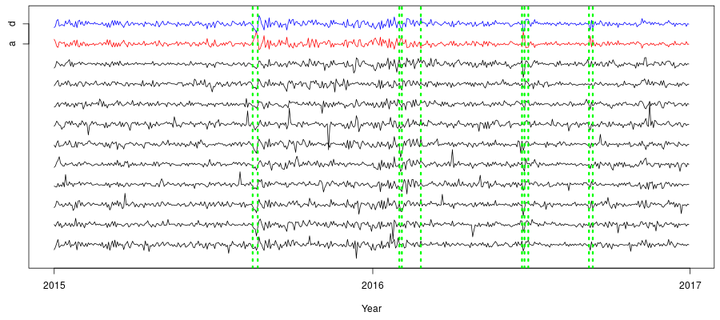
 Segmentation of S&P500 data
Segmentation of S&P500 dataAbstract
High-dimensional changepoint analysis is a growing area of research and has applications in a wide range of fields. The aim is to accurately and efficiently detect changepoints in time series data when both the number of time points and dimensions grow large. Existing methods typically aggregate or project the data to a smaller number of dimensions, usually one. We present a high-dimensional changepoint detection method that takes inspiration from geometry to map a high-dimensional time series to two dimensions. We show theoretically and through simulation that if the input series is Gaussian, then the mappings preserve the Gaussianity of the data. Applying univariate changepoint detection methods to both mapped series allows the detection of changepoints that correspond to changes in the mean and variance of the original time series. We demonstrate that this approach outperforms the current state-of-the-art multivariate changepoint methods in terms of accuracy of detected changepoints and computational efficiency. We conclude with applications from genetics and finance.